We want to highlight in a graph some subsets with important connectivity properties, the cores. We described what these cores are in detail in a previous post. But how do we break down a graph in its cores? To partition the graph there is an interesting recursive algorithm, called k-pruning and I will describe here how it works. I also wrote some code in C programming language, to perform this decomposition on a general undirected graph, given its representation as a list of edges in a text file. If you are interested you can find this C code here in my repository (under kCores folder).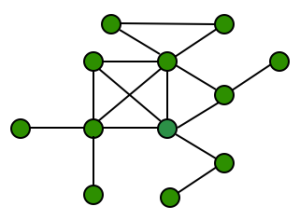
Let’s now consider a cyclic undirected graph, green vertices in the figure above. From the definition of k-core we have that every vertex with degree ≥ k belongs to the k-core. We notice that every vertex in this graph has degree ≥ 1, thus the whole graph should be a 1-core.
The algorithm of the k-pruning says: remove recursively all vertices with degree < k, the remaining vertices belong to the k-core. In order to have all the possible cores of the graph, we have to perform this recursive pruning for k going from the minimum degree of the graph to the maximum degree. In this case we have minimum 1 and maximum 6. According to this procedure, we can see that there are no isolated vertices, with degree < 1, thus the whole graph is a 1-core, as we already noticed.
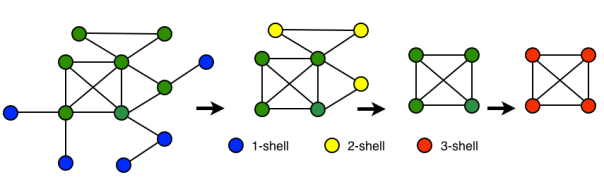We now remove recursively all vertices with degree < 2, the vertices in blue in the figure above. We obtain the 2-core (remaining green vertices). The blue vertices belong to the 1-core but not to the 2-core, thus they are the 1-shell (see here for definitions and more details). Same happens for the vertices with degree < 3, in yellow in the figure above. They are removed recursively and we obtain the 2-shell, and the remaining vertices belong to the 3-core. We notice now that removing all vertices with degree < 4 we have nothing left. That means that the we have no more inner cores to find.
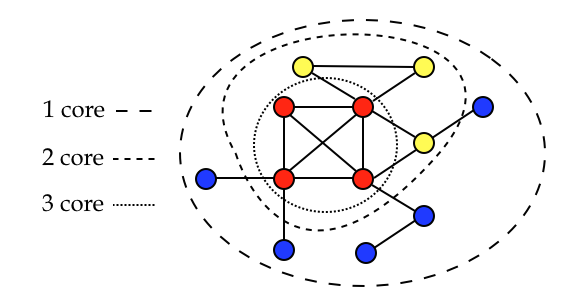
We did not perform the pruning for all values of allowed k, from minimum degree 2 to maximum degree 6. With degree 4 we already found no vertices left. This gives us an idea of how many and strong connections should be in a graph, in order to resist to a pruning with an high value of k. Therefore the core decomposition of a graph gives us very different results depending on the degree distribution.
chaos like home 